math

Natural Numbers

Peano Axioms

• (Axiom 2.1) Zero
  • 0 is a natural number
• (Axiom 2.2) $++$, the increment operation
  • if $n$ is a natrual number, then $n++$ is also a natural number.
• (Axiom 2.3) $0$ is the first
  • $n++ \neq 0$ for every natrual number n
• (Axiom 2.4) Uniqueness of increment
  • $n \neq m \implies n++ \neq m++$
• (Axiom 2.5) Principal of mathimatical induction
  • $[P(0) \land (P(n) \implies P(n++))] \implies [\forall n P(n)]$
    • $P(n)$ is a property pertaining to natural number $n$
• (Definition 2.2.7) Positive natural
  • $n$ is positive $\iff n \neq 0$
• (Corollary 2.2.9) $a + b = 0 \implies a = 0 \land b = 0$
• (Lemma 2.2.10) $a > 0 \implies (\exists ! b) b++ = a$
• (Proposition 2.2.14) Strong principal of induction
  • $(\forall m \ge m_0) [[(\forall m_0 \le m’ < m) P(m’) \implies P(m)] \implies (\forall m \ge m_0) P(m)]$
    • $m_0$ is any natrual number, $P(m)$ is a property pertaining to natural number $m$
  • Break down version:
    • $\forall m_0 [(\forall m \ge m_0) Q(m) \implies (\forall m \ge m_0) P(m)]$
    • $Q(m)$ is defined as:
      • $(\forall m_0 \le m’ < m) P(m’) \implies P(m)$

Precedence of logical operator

The convention is described by Herbert Enderton in A Mathematical Introduction to Logic page 78.

Operator	Name	Precedence
$\forall$, $\exists$	Modifier	Highest, apply to as little as possible
$\lnot$	Negation	Highest, apply to as little as possible
$\land$	Conjunction
$\lor$	Disjunction
$\implies$	Implication	Right associative
$\iff$	Biconditional

• Examples (todo: Not convinced!!!)
  • $¬α ∧ β$ is $((¬α) ∧ β)$, and not $¬(α ∧ β)$
  • $∀x α → β$ is $(∀x α) → β$, and not $∀x(α → β)$
  • $∃x α ∧ β$ is $(∃x α) ∧ β$, and not $∃x(α ∧ β)$.
  • $α → β → γ$ is $α → (β → γ)$.

Logic

• $\forall$ Equivalent
  • $(\forall x \in X) Q(x)$
  • $\forall x [x \in X \implies Q(x)]$
• $\exists$ Equivalent
  • $(\exists x \in X) Q(x)$
  • $\exists x [x \in X \land Q(x)]$

Axioms of Equality (A.7)

How equality is defined depends on the class type of objects under consideration. But all equality definition should obey the following four axioms of equality:

1. Reflexive axiom.
   • Given any object x, we have x = x.
2. Symmetry axiom.
   • Given any two objects x and y of the same type, if x = y, then y = x.
3. Transitive axiom.
   • Given any three objects x, y, z of the same type, if x = y and y = z, then x = z.
4. Substitution axiom.
   • Given any two objects x and y of the same type, if x = y, then f(x) = f(y) for all functions or operations f.
   • Similarly, for any property P(x) depending on x, if x = y, then P(x) and P(y) are equivalent statements.
   • Note, when introducing an opertion to objects of type T, it’s considered a well-defined operation only if it follows the Substitution axiom.

Set Theory

Axiom vs. Definition

An axiom is a assumption/rule that we decide we will follow/enforce. Axioms come mainly in two different kinds: existential and universal.

1. Existential: there exists an empty set
2. Universal: all right angles are equal (?)

ZFC Axiom of Set Theory

• (Definition 3.1.1) Informal Set
  • A set is unordered collection of objects(*)
  • If $x$ is an object, then
    • $x$ is an element(*) of set A, i.e. $x \in A$, if $x$ lies in the collection
    • $x \notin A$, if $x$ does not lie in the collection
• (Axiom 3.1) Sets are objects
  • A is a set => A is an object
    • In particular, given set A and B, it’s meaningful to ask if $A \in B$
• (Definition 3.1.4) Equality
  • $A = B \iff \forall x [(x \in A \implies x \in B) \land (x \in B \implies x \in A)]$
• (Axiom 3.2) Empty set exists
  • $(\exists \emptyset) (\forall \ object \ x ) x \notin \emptyset$
• (Lemma 3.1.6) Single choice
  • $A \neq \emptyset \implies \exists x (x \in A)$
  • Note: the antecedent assumes non empty set A exists. this lemma does NOT prove that A exists
• (Axiom 3.3) Singleton/pair sets exist
  • Singleton $\lbrace a \rbrace$: $\forall (object \ a) \exists A \forall (object \ y) (y \in A \iff y = a)$
  • Pair $\lbrace a, b \rbrace$: $\forall (object \ a) \forall (object \ b) \exists A \forall (object \ y)(y \in A \iff y = a \lor y = b)$
• (Axiom 3.4) Pairwise union exists
  • $\forall A \forall B [A \cup B \ exists]$
  • $A \cup B$ is defined as:
    • $\forall x (x \in A \cup B \iff x \in A \lor x \in B)$
• (Defnition 3.1.15) Subsets
  • $A \subseteq B \iff \forall \ object \ x (x \in A \implies x \in B)$
• (Axiom 3.5) Axiom of specification/separation
  • Set $\lbrace x \in A \mid P(x) \rbrace$ exists
  • And it’s defined as: $(\forall y) [y \in \lbrace x \in A \mid P(x) \rbrace \iff y \in A \land P(y)]$
• (Defnition 3.1.23) Intersections
  • $S_1 \cap S_2 := \lbrace x \in S_1 \mid x\in S_2 \rbrace$
  • In other words: $x \in S_1 \cap S_2 \iff x \in S_1 \land x\in S_2$
• (Defnition 3.1.27) Difference Sets
  • $A \backslash B := \lbrace x \in A \mid x\notin B \rbrace$
• (Axiom 3.6) Replacement
  • $(\forall x \in A) \forall y \lbrace [\forall y_1 \forall y_2 (P(x,y1) \land P(x,y2) \implies y_1 = y_2)] \implies Set \ \lbrace y \mid (\exists x \in A) P(x,y) \rbrace \ exists \rbrace$
    • Informal: $(\forall x \in A) \forall y [\text{at most one y for any x, s.t. P(x,y) holds} \implies \ \lbrace y \mid (\exists x \in A) P(x,y) \rbrace \text{exists}]$
  • $z \in \lbrace y \mid (\exists x \in A) P(x,y) \rbrace \iff (\exists x \in A) P(x,z)$
• (Axiom 3.7) Infinity
  • $\mathbb{N}$ exists, and its elements are called natural numbers.
  • $0 \in \mathbb{N} \land (n \in \mathbb{N} \implies n++ \in \mathbb{N})$ and Peano Axiom holds
• (Axiom 3.8) Universal specification (Not chosen)
  • $\forall P [\forall x P(x) \ exists \implies \lbrace x \mid P(x) \rbrace \ exists]$
  • And it’s defined as: $(\forall y) [y \in \lbrace x \mid P(x) \rbrace \iff P(y) \ is \ true]$
• (Axiom 3.9) Regularity/Foundation
  • $(\forall set A \neq \emptyset) (\exists x \in A) [x \ is \ not \ a \ set \lor x \cap A = \emptyset]$
• (Axiom 3.10) Power set
  • $(\forall set X) (\forall set Y) (Y^X \ exists)$
  • $Y^X := \lbrace f \mid f: X \to Y \rbrace$
    • $f \in Y^X \iff f \text{ is a function with domain X and range Y}$
• (Axiom 3.11) Union
  • $(\forall x \in A) [x \ is \ a \ set] \implies \bigcup A \ exists$
  • $\bigcup A$ is defined as:
    • $x \in \bigcup A \iff (\exists S \in A) x \in S$
  • $\bigcup_{\alpha \in I} A_{\alpha} := \bigcup\lbrace A_\alpha \mid \alpha \in I \rbrace$
    • $x \in \bigcup_{\alpha \in I} A_{\alpha} \iff (\exists \alpha \in I) x \in A_\alpha$
  • $\bigcap_{\alpha \in I} A_{\alpha} := \lbrace x \in A_\beta \mid (\forall \alpha \in I) x \in A_\alpha \rbrace$
    • $x \in \bigcap_{\alpha \in I} A_{\alpha} \iff (\forall \alpha \in I) y \in A_\alpha$

Functions

• (Definition 3.3.1) Functions
  • $f: X \to Y$ is defined as:
    • $(\forall set X) (\forall set Y) [(\forall x \in X) (\exists! y \in Y )P(x, y) \implies (\exists f: X \to Y) (\forall x \in X) (\exists! f(x) \in Y) P(x, f(x))]$
• (Definition 3.3.7) Equality of Functions
  • Consider two functions $f : X \to Y$ and $g : X \to Y$
    • Note $f$ and $g$ have the same domain and range.
  • $f = g \iff (\forall x \in X) [f(x) = g(x)]$
• (Definition 3.3.10) Composition
  • Consider two functions $f : X \to Y$ and $g : Y \to Z$
  • $(g \circ f)(x):= g(f(x))$
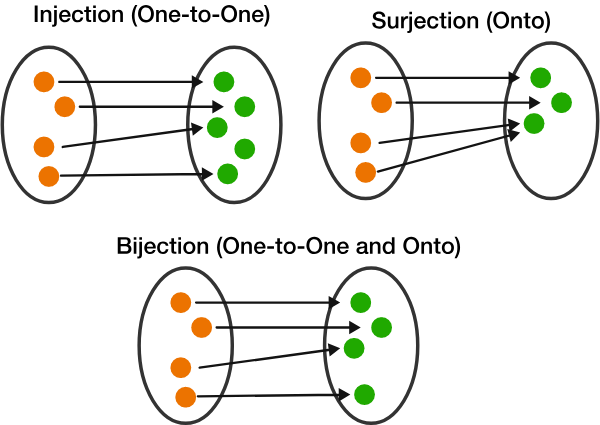
• (Definition 3.3.14) One-to-one functions (injective)
  • $x \neq x’ \implies f(x) \neq f(x’)$
• (Definition 3.3.17) Onto functions (Surjective)
  • Often written as $f(X) = Y$
  • $(\forall y \in Y) (\exists x \in X) f(x) = y$
• (Definition 3.3.20) Bijective functions (invertible)
  • both bijective and surjective; also called “perfect matching”, “one to one correspondence”.
  • $(\forall y \in Y) (\exists! x \in X) f(x) = y$
    • At least one $x$ because of surjectivity, and at most one $x$ because of injectivity
  • $(\forall x \in X) (\exists! y \in Y) f(x) = y$ by definition of “function”
  • 
• (Excercise 3.3.8) Inclusion map (iota)
  • $X \subseteq Y$, Inclusion map $\iota_{X \to Y}: X \to Y$ is defined as:
  • $(\forall x \in X) \iota_{X \to Y}(x):=x$
  • Identity map: $\iota_{X \to X}: X \to X$
• (Definition 3.4.1) Image of sets
  • $f(S) := \lbrace f(x) \mid x \in S \rbrace$
    • $ \mid $ reads: “for some”
    • $y \in f(S) \iff (\exists x \in X) y = f(x)$
    • $f : X \to Y$, $S \subseteq X$, $f(S) \subseteq Y$
• (Definition 3.4.4) Inverse Images
  • $f^{-1}(U) := \lbrace x \in X \mid f(x) \in U \rbrace$
    • $ \mid $ reads: “such that”, “and”
    • $x \in f^{-1}(U) \iff f(x) \in U$
    • $f : X \to Y$, $U \subseteq Y$
• Function and set with $ \mid $
  • (Axiom 3.5 Specification) Set $\lbrace x \in A \mid P(x) \rbrace$ exists
  • (Axiom 3.6 Replacement) Set $\lbrace y \mid (\exists x \in A) P(x,y) \rbrace$ exists
    • $z \in \lbrace y \mid (\exists x \in A) P(x,y) \rbrace \iff (\exists x \in A) P(x,z)$
  • (Example 3.1.32) $\lbrace f(x) \mid x \in A \rbrace$
    • shorthand for: $\lbrace y \mid y = f(x) \text{ for some } x \in A \rbrace$
    • $y \in \lbrace f(x) \mid x \in A \rbrace \iff (\exists x \in A) y = f(x)$
  • (Definition 3.4.1) $f(S) := \lbrace f(x) \mid x \in S \rbrace$

Cartesian Product of Set

• (Definition 3.5.1) Ordered pair
  • Ordered pair exists: $\forall x \forall y \exists (x,y)$
    • Proof by construction: $(x, y) := \lbrace \lbrace x \rbrace, \lbrace x, y \rbrace \rbrace$
  • Ordered pair equality: $(x, y) = (x’, y’) \iff x = x’ \land y = y’$
• (Definition 3.5.4) Cartesian Product (Collection of ordered pairs)
  • $X \times Y := \lbrace (x, y) \mid x \in X \land y \in Y \rbrace$
    • $X \times Y$ is a set, and it exists.
    • $ \mid $ reads “for some”
    • $a \in (X \times Y) \iff (\exists x \in X) (\exists y \in Y) a = (x, y)$
• (Definition 3.5.7) Ordered n-tuple and n-fold cartesian product
  • Ordered n-tuple
    • Notation
      • $(x_i)_{1 \leq i \leq n}$
      • $(x_1, …, x_n)$
    • Equality
      • $(x_i){1 \leq i \leq n} = (y_i){1 \leq i \leq n} \iff (\forall i \in \lbrace 1,…,n \rbrace) x_i = y_i$
  • N-fold cartesian product (of an ordered n-tuple of sets)
    • Notation
      • $X^n$
      • $\prod_{1 \leq i \leq n} X_i$
      • $\prod_{i=1}^n X_i$
      • $(X_1 \times … \times X_n)$
    • Definition
      • $\prod_{1 \leq i \leq n} X_i := \lbrace (x_i)_{1 \leq i \leq n} \mid (\forall i \in \lbrace 1,…,n \rbrace) x_i \in X_i \rbrace$
        • $a \in \prod_{1 \leq i \leq n} X_i \iff [(\forall i) [(1 \leq i \leq n) \implies(\exists x_i) x_i \in X_i]] \land a = (x_j)_{1 \leq j \leq n}$
• (Excercise 3.5.7) Coordinate Function and Direct Sum
  • Coordinate functions on $X \times Y$
    • $\pi_{X \times Y \to X} : X \times Y \to X$ and $\pi_{X \times Y \to X}(x,y) := x$
    • $\pi_{X \times Y \to Y} : X \times Y \to Y$ and $\pi_{X \times Y \to Y}(x,y) := y$
  • $(\forall f : Z \to X) (\forall g : Z \to Y) (\exists! h : Z \to X \times Y) \pi_{X \times Y \to X} \circ h= f \land \pi_{X \times Y \to Y} \circ h= g$
    • $h$ is the direct sum of $f$ and $g$, denoted $h := f \bigoplus g$
• (Excercise 3.5.10) Graph
  • $f : X \to Y$ is a function
  • Graph of $f$ is a set: $\lbrace (x, f(x)) \mid x \in X \rbrace$
• (Definition 3.6.1) Equal cardinality of two sets
  • $X$ and $Y$ have equal cardinality $\iff$ there exists a bijection $f : X \to Y$
• (Definition 3.6.5) Assign cardinality of set $X$ to a natural number $n$
  • $X$ has cardinality $n$ $\iff$ $X$ has equal cardinality with ${i \in N \mid 1 \leq i \leq n }$
• (Definition 3.6.10) finite sets
  • Set $X$ is finite $\iff$ $X$ has cardinality $n$ for some natural number $n$
    • $#(X) := n$

Integers

• (Definition 4.1.1) Integers
  • $a,b,c,d \in N$ Define equivalence relation ~ on $N \times N$
    • $(a, b) \sim (c, d) \iff a + d = c + b$
  • $a – b := \lbrace (c, d) \in N \times N \mid (a, b) \sim (c, d) \rbrace$
    • integer is defined as a set of equivalent ordered pairs of natural numbers
  • Let $Z$ denote all set of integers.
• (Definition 4.1.2) Integer operations
  • Sum of two
    • $(a–b) + (c–d) := (a+c) – (b+d)$
      • well-defined:
      • if $(a–b) = (a’–b’)$, to show $(a–b) + (c–d) = (a’–b’) + (c–d)$
        • By “+” definition, $LHS = (a+c) – (b+d)$ and $RHS = (a’+c) – (b’+d)$
        • To prove LHS = RHS is to show $(a+c)+(b’+d)=(a’+c)+(b+d)$
        • use $(a–b) = (a’–b’) \iff a+b’=a’+b$
  • Product of two
    • $(a–b) \times (c–d) := (ac+bd) – (ad+bc)$
• (Lemma 4.1.3) Integer addition and multiplication are well defined
  • Need check Substitution Axiom holds when defining new operations (+, x) on new class (integer)
  • Equal inputs give equal outputs
    • If $a–b = a’–b’$, then
      • $(a–b) + (c–d) = (a’–b’) + (c–d)$
      • $(a–b) \times (c–d) = (a’–b’) \times (c–d)$
      • $(c–d) + (a–b) = (c–d) + (a’–b’)$
      • $(c–d) \times (a–b) = (c–d) \times (a’–b’)$
• Isomorphism $n \equiv n–0$. This is valid because:
  • $n = m \iff (n–0) = (m–0)$
    • Every natural number $n$ can be mapped to a unique integer $n–0$.
  • $(n–0) + (m–0) = (n+m)–0$
  • $(n–0) \times (m–0) = (n \times m)–0$
    • let a, b, c be natural numbers; let A, B, C be integers; let a “identifies” A and let b “identifies” B. let c = a + b, and C = A + B.
    • It happens that c “identifies” C.
• (Definition 4.1.4) Negation of integers
  • $-(a–b) := (b–a)$
  • In particular: $-(n–0)=(0–n)$, which can be written as $-n=(0–n)$
  • Under this definition, it happens that
    • $-(a–b)=(0–1) \times (a–b)$
    • 负负得正 $(-n) \times (-m) = (0–n) \times (0–m) = (nm – 0) = nm$
• (Definition 4.1.4+) Subtraction of integers
  • $x-y := x + (-y)$
  • Check isomorphism on natural numbers a, b:
    • $a - b = a + (-b) = (a–0) + (0–b) = a–b$
• (Lemma 4.1.5) Trichotomy of integers
  • Exactly one statements out three in the following is true about integer $x$.
    • $x$ is zero;
    • $x$ is equal to a positive natural number n;
    • $x$ is the negation $-n$ of a positive natural number $n$
• (Proposition 4.1.6) Laws of algebra for integers
  • $Z$ forms a Commutative ring
    1. $x + y = y + x$
    2. $(x + y) + z = x + (y + z)$
    3. $x + 0 = 0 + x = x$
    4. $x + (-x) = (-x) + x = 0$
    5. $xy = yx$
    6. $x(yz) = (xy)z$
    7. $x1 = 1x = x$
    8. $x(y+z) = xy + xz$
    9. $(y+z)x = yx + zx$
• (Proposition 4.1.8) Integers have no zero divisors
  • $ab = 0 \implies a = 0 \lor b=0$
• (Corollary 4.1.9) Cancellation law for integers
  • $ac = bc \land c \neq 0 \implies a = b$
• (Definition 4.1.10) Ordering of integers
  • $n \geq m \iff (\exists a \in N) n = m + a$
    • $n \geq m \iff m \leq n$
  • $n \gt m \iff n \geq m \land n \neq m$
• (Lemma 4.1.11) Properties of order
  1. $a > b \iff a - b \in N^+$
  2. (Addition preserves order) $ a > b \implies a + c > b + c$
  3. (Positive multiplication preserves order) $a > b \land c > 0 \implies ac > bc$
  4. (Negation reverses order) $a > b \implies -a < -b$
  5. (Order is transitive) $a > b \land b > c \implies a > c$
  6. (Order trichotomy) Exact one of the statements is true: $a > b, a < b, a = b$

Rationals

• (Definition 4.2.1) Rationals
  • Define equivalence relation ~ on $Z \times (Z \setminus {0})$
    • $(a, b) \sim (c, d) \iff ad = cb$
  • $(a,b) \in Z \times (Z \setminus {0})$, denote $a // b := \lbrace (c, d) \in Z \times (Z \setminus {0}) \mid (a, b) \sim (c, d) \rbrace$
    • rational is defined as a set of equivalent ordered pairs of integers
  • Let $Q$ denote all set of rationals.
• (Definition 4.2.2) Rationals’ sum, product and negation
  • $a//b + c//d := (ad + bc) // (bd)$
  • $(a//b) \times (c//d) := (ac) // (bd)$
    • Observe the result is also a rational. $b \neq 0 \land d \neq 0 \implies bd \neq 0$ by Prop 4.1.8 (Excercise 4.1.5)
  • $-(a//b) = (-a)//b$
• (Lemma 4.2.3) Definition 4.2.2 is well defined
• Isomorphism $a \equiv a//1$ for any integer $a$. This is valid because:
  • $a = b \iff (a//1) = (b//1)$
    • Equiality definition is consistent with integers
  • $(a//1) + (b//1) = (a+b)//1$
  • $(a//1) \times (b//1) = (ab)//1$
  • $-(a//1) = (-a)//1$
    • Arithmetic of integers is consistent with arithmetic of rationals.
• (Lemma 4.2.3+) Reciprocal
  • $x = a//b$ where $a \neq 0 \land b \neq 0$
  • $x^{-1} := b//a$
• (Proposition 4.2.4) Laws of algebra for rationals
  • $Q$ forms a Field
    1. $x + y = y + x$
    2. $(x + y) + z = x + (y + z)$
    3. $x + 0 = 0 + x = x$
    4. $x + (-x) = (-x) + x = 0$
    5. $xy = yx$
    6. $x(yz) = (xy)z$
    7. $x1 = 1x = x$
    8. $x(y+z) = xy + xz$
    9. $(y+z)x = yx + zx$
    10. $xx^{-1} = x^{-1}x= 1$, when $x \neq 0$
• (Proposition 4.2.4+) Quotient/substractions of rationals
  • $x/y := x \times y^{-1}$, when $y \neq 0$
  • $x-y := x + (-y)$
• (Definition 4.2.6) Positive and negative rationals
  • A rational number $x$ is positive iff:
    • $(\exists a \in Z^+)(\exists b \in Z^+) x = a/b$
    • $Z^+ := {x \mid x \in Z \land x > 0}$
  • A rational number $x$ is negative iff:
    • $(\exists y \in Q)(\exists a \in Z^+)(\exists b \in Z^+) (y = a/b \land x = -y)$
• (Lemma 4.2.7) Trichotomy of rationals
  • Let $x$ be a rational number, exact one of the three statement is true
    1. $x$ is equal to zero,
    2. $x$ is a positive rational number,
    3. $x$ is a negative rational number.
• (Definition 4.2.8) Ordering of rationals
  • $x > y \iff x - y \text{ is a positive rational number}$
    • $x >= y \iff x - y \lor x = y$
  • $x < y \iff x - y \text{ is a negative rational number}$
• (Proposition 4.2.9) Properties of order on rationals (Ordered field)
  1. Order Trichotomy. Exactly one of three is true: $x = y$, $x < y$, or $x > y$
  2. Order is anti-symmetric. $x < y \iff y > x$
  3. Order is transitive. $x < y \land y < z \implies x < z$
  4. Addition preserves order. $x < y \implies x + z < y + z$
  5. Positive multiplication preserves order. $x < y \land z \text{ is positive } \implies xz < yz$

     Absolute value and exponentiation

• (Definition 4.3.1) Absolute value
  • $\vert x \vert := x$, if $x$ is positive
  • $\vert x \vert := -x$, if $x$ is negative
  • $\vert x \vert := 0$, if $x$ is 0
• (Definition 4.3.2) Distance
  • $d(x,y) := \vert x - y \vert $
• (Proposition 4.3.3) Properties of absolute and distance
  • Absolute
    1. (Non-degeneracy) $\vert x \vert \geq 0$, also $\vert x \vert = 0 \iff x = 0$
    2. (Triangle inequality) $\vert x+y \vert \leq \vert x \vert + \vert y \vert$
    3. $-y \leq x \leq y \iff y \geq \vert x \vert$
       1. In particular: $-\vert x \vert \leq x \leq \vert x \vert$
    4. (Multiplicativity) $\vert xy \vert = \vert x \vert \cdot \vert y \vert$
       1. In particular: $\vert -x \vert = \vert x \vert$
  • Distance
    1. (Non-degeneracy) $d(x,y) \geq 0$, also $d(x,y) = 0 \iff x = y$
    2. (Symmetry) $d(x,y) = d(y,x)$
    3. (Triangle inequality) $d(x,z) \leq d(x,y) + d(y,z)$
• (Definition 4.3.4) $\epsilon$-closeness
  • $y$ is $\epsilon$-close to $x$ $\iff d(y,x) \leq \epsilon$
• (Definition 4.3.9) Exponetiation to a natural number
  • $x^0 := 1$
  • $x^{n+1} := x^n \times x$
• (Definition 4.3.11) Exponetiation to a negative integer
  • $x \neq 0$ and for any negative integer $-n$:
  • $x^{-n} := 1/x^n$
• (Definition 4.3.12) Properties of exponetiation, Let $x, y \in Q \land x, y \neq 0 \land n, m \in Z$
  • $x^nx^m = x^{n+m}$, $(x^n)^m = x^{nm}$, $(xy)^n = x^n y^n$
  • $ n > 0 \land x \geq y \gt 0 \implies x^n \geq y^n \gt 0$
    • $ n < 0 \land x \geq y \gt 0 \implies 0 \lt x^n \leq y^n$
  • $x, y > 0 \land n \neq 0 \land x^n = y^n \implies x = y$
  • $\vert x^n \vert = \vert x \vert^n$

Gaps in rationals

• (Proposition 4.4.1) Interspersing of integers by rationals
  • $(\forall x \in Q) (\exists! n \in Z) n \leq x \lt n+1$
  • (Remark 4.4.2) integer part $n = \lfloor x \rfloor$
• (Proposition 4.4.3) Interspersing of rationals by rationals
  • $(\forall x \in Q)(\forall y \in Q)[x \lt y \implies (\exists z \in Q) x \lt z \lt y]$
• (Proposition 4.4.4+) Even and odd natural number
  • Given $p \in N$
    • $(\exists k \in N) p = 2k$
    • $(\exists k \in N) p = 2k+1$

Reals

Cauchy sequences

• (Definition 5.1.1) Sequences
  • $m$ is an integer, a sequence $(a_n)_{n=m}^\infty$ of rational numbers is any function $f$:
  • $f: {n \in Z : n \geq m} \to Q$
• (Definition 5.1.8) Cauchy sequences
  • A sequence $(a_n)_{n=0}^\infty$ of rational numbers is a Cauchy squence iff:
  • $(\forall \epsilon > 0)(\exists N \geq 0) (\forall j \geq N) (\forall k \geq N) [d(a_j, a_k) \leq \epsilon]$
• (Definition 5.1.12) Bounded sequences
  • Let $M \geq 0$ be rational.
  • A finite sequence $(a_i)_{i=0}^n$ is bounded by $M$ iff:
    • $(\forall i \in [0, n]) [\vert a_i \vert \leq M]$
  • A infinite sequence $(a_i)_{i=0}^\infty$ is bounded by $M$ iff:
    • $(\forall i \geq 0) [ \vert a_i \vert \leq M]$
  • A sequence is bounded iff it’s bounded by $M$ for some $M \geq 0$
• (Lemma 5.1.14) Every finite sequence is bounded
• (Lemma 5.1.15) Every Cauchy sequence $(a_n)_{n=0}^\infty$ is bounded
• (Definition 5.2.6) Equivalent sequences
  • Two sequences $(a_n){n=0}^\infty$ and $(b_n){n=0}^\infty$ are equivalent iff:
    • $(\forall \epsilon > 0) (\exists N \geq 0) (\forall n \geq N) \vert a_n - b_n \vert \leq \epsilon$

Construction of real

• (Definition 5.3.1) Real numbers
  • A real number is defined to be an object of form $LIM_{n \rightarrow \infty}a_n$
    • where $(a_n)_{n=0}^\infty$ is a Cauchy sequence of rational numbers
  • Two real numbers $LIM_{n \rightarrow \infty}a_n$ and $LIM_{n \rightarrow \infty}b_n$ are said to be equal iff:
    • $(a_n){n=0}^\infty$ and $(b_n){n=0}^\infty$ are equivalent Cauchy sequences.
• (Proposition 5.3.3) Formal limits are well defined
  • Reflexive: $x = x$
  • Symmetric: $x = y \iff y = x$
  • Transitive: $x = y \land y = z \implies x = z$
• (Definition 5.3.4) Addition
  • let $x = LIM_{n \rightarrow \infty}a_n$ and $y = LIM_{n \rightarrow \infty}b_n$
  • $x + y := LIM_{n \rightarrow \infty}(a_n + b_n)$
• (Lemma 5.3.6) Addition of two real number is also a real number
• (Lemma 5.3.7) Addition obeys Axiom of substitution
  • $x = x’ \implies x + y = x’ + y$
• (Definition 5.3.9) Multiplication
  • let $x = LIM_{n \rightarrow \infty}a_n$ and $y = LIM_{n \rightarrow \infty}b_n$
  • $xy := LIM_{n \rightarrow \infty}(a_nb_n)$
• (Proposition 5.3.10) Multiplication is well defined
  • Multiplication of two real number is also a real number
  • Multiplication obeys Axiom of substitution, i.e. $x=x’ \implies xy = x’y$
• (Proposition 5.3.10+) Embed rational in real
  • Isomorphism $q \equiv LIM_{n \rightarrow \infty}q$ for any rational $q$. This is valid because:
    • $a = b \iff LIM_{n \rightarrow \infty}a = LIM_{n \rightarrow \infty}b$
    • $LIM_{n \rightarrow \infty}a + LIM_{n \rightarrow \infty}b = LIM_{n \rightarrow \infty}(a + b)$
    • $LIM_{n \rightarrow \infty}a \times LIM_{n \rightarrow \infty}b = LIM_{n \rightarrow \infty}(a \times b)$
    • Thus when add, multiply or equal-compare two rationals, it doesn’t matter whether one thinks it as rational numbers $a$ or as real numbers $LIM_{n \rightarrow \infty}a$
• (Definition 5.3.10+) Extended operations
  • Negation: $-x := (-1) \times x$
  • Subtraction: $x-y := x + (-y)$
• (Proposition 5.3.11) Laws of algebra as integer Proposition 4.1.6
  • $R$ forms a Commutative ring
    1. $x + y = y + x$
    2. $(x + y) + z = x + (y + z)$
    3. $x + 0 = 0 + x = x$
    4. $x + (-x) = (-x) + x = 0$
    5. $xy = yx$
    6. $x(yz) = (xy)z$
    7. $x1 = 1x = x$
    8. $x(y+z) = xy + xz$
    9. $(y+z)x = yx + zx$
• (Definition 5.3.12) Sequence bounded away from 0
  • A sequence $(a_n)_{n=0}^\infty$ of rationals is said to be founded away from zero iff:
    • $(\exists c \in Q^+) (\forall n \in N) \vert a_n \vert \geq c$
• (Lemma 5.3.14) Non 0 is bounded away from 0
  • Let $x$ be a real number, let $s = (a_n)_{n=0}^\infty$ be a sequence
  • $x \neq 0 \implies (\exists s) [s = (a_n){n=0}^\infty \land \text{ s is Cauchy} \land \text{ s is bounded away from zero} \land x = LIM{n \rightarrow \infty}a_n ]$
• (Lemma 5.3.15) Reciprocal is Cauchy
  • $(a_n){n=0}^\infty \text{ is Cauchy sequence which is bounded away from 0} \implies (a_n^{-1}){n=0}^\infty \text{ is also Cauchy}$
• (Definition 5.3.16) Reciprocals of real
  • Let $x \neq 0 \land x = LIM_{n \rightarrow \infty}a_n$
    • By lemma 5.3.14, $(a_n)_{n=0}^\infty$ exists and is Cauchy and is bounded away from 0.
  • Define reciprocal $x^{-1} := LIM_{n \rightarrow \infty}a_n^{-1}$
    • By lemma 5.3.15, $(a_n^{-1}){n=0}^\infty$ is Cauchy thus we can have $LIM{n \rightarrow \infty}a_n^{-1}$
• (Lemma 5.3.17) Reciprocation is well defined
  • Let $(a_n){n=0}^\infty$ and $(b_n){n=0}^\infty$ be two Cauchy sequences bounded away from 0, then:
  • $LIM_{n \rightarrow \infty}a_n = LIM_{n \rightarrow \infty}b_n \implies LIM_{n \rightarrow \infty}a_n^{-1} = LIM_{n \rightarrow \infty}b_n^{-1} $
• (Lemma 5.3.17+) $R$ forms a Field (since $xx^{-1} = x^{-1}x = 1$)
• (Lemma 5.3.17+) Extended operations
  • Division: $x/y := x \times y^{-1}$

Ordering of real

• (Definition 5.4.1) Positive/negative bounded away from zero
  • Let $(a_n)_{n=0}^\infty$ be a sequence of rationals. $c \in Q$, $n \in N$
  • Positively bounded away from zero iff:
    • $(\exists c > 0) (\forall n) a_n \geq c$
  • Negatively bounded away from zero iff:
    • $(\exists -c < 0) (\forall n) a_n \leq -c$
• (Definition 5.4.3) Positive/negative real numbers
  • $x$ is positive iff:
    • $(\exists s) [s = (a_n){n=0}^\infty \land \text{ s is Cauchy} \land \text{ s is positively bounded away from zero} \land x = LIM{n \rightarrow \infty}a_n ]$
  • $x$ is negative iff:
    • $(\exists s) [s = (a_n){n=0}^\infty \land \text{ s is Cauchy} \land \text{ s is negatively bounded away from zero} \land x = LIM{n \rightarrow \infty}a_n ]$
• (Proposition 5.4.4) Properties of positive reals
  • Trichotomy: for real number $x$, exact one of three is true:
    1. $x$ is zero
    2. $x$ is postive
    3. $x$ is negative
  • $x$ is negative $\iff$ $-x$ is positive
  • $x$, $y$ are positive $\implies$ $x+y$, $xy$ are positive
• (Definition 5.4.5) Absolute value of real $x$
  • $\vert x \vert := \begin{cases} x, & x \text{ is positive} \ -x, & x \text{ is negative}
    0, & x \text{ is zero} \end{cases} $
• (Definition 5.4.6) Ordering of real $x, y$
  • $x>y \iff x-y \text{ is positive}$
    • $x \geq y \iff x > y \lor x = y$
  • $x<y \iff x-y \text{ is negative}$
    • $x \leq y \iff x < y \lor x = y$
• (Proposition 5.4.7) Properties of order on reals (Ordered field), same as Proposition 4.2.9.
  1. Order Trichotomy. Exactly one of three is true: $x = y$, $x < y$, or $x > y$
  2. Order is anti-symmetric. $x < y \iff y > x$
  3. Order is transitive. $x < y \land y < z \implies x < z$
  4. Addition preserves order. $x < y \implies x + z < y + z$
  5. Positive multiplication preserves order. $x < y \land z \text{ is positive } \implies xz < yz$
• (Proposition 5.4.8) Positive reciprocal reverses order
  • $x > 0 \implies x^{-1} > 0$
  • $x > 0 \land y > 0 \land x > y \implies x^{-1} < y^{-1}$
• (Proposition 5.4.9) Non-negative reals are closed
  • $x > 0 \implies x^{-1} > 0$
  • $(a_n){n=0}^\infty \text{ is Cauchy } \land (\forall n) a_n \geq 0 \implies LIM{n \rightarrow \infty}a_n \geq 0$
• (Corollary 5.4.10) LIM preserves order
  • Let $(a_n){n=0}^\infty$ and $(b_n){n=0}^\infty$ be Cauchy sequences of rationals.
  • $(\forall n \in N) a_n \geq b_n \implies LIM_{n \rightarrow \infty}a_n \geq LIM_{n \rightarrow \infty}b_n$
• (Proposition 5.4.12) Bounding of reals by rationals
  • $x \in R^+ \implies (\exists q \in Q^+) (\exists n \in N^+) q \leq x \leq n$
• (Corrollary 5.4.13) Archimedian Property
  • $x, \epsilon \in R^+ \implies (\exists M \in N^+) M \epsilon > x $
• (Corrollary 5.4.14) Interspersing of reals by rationals
  • $(\forall x,y \in R) x < y \implies (\exists q \in Q) x < q < y$
• (Excercise 5.4.3) Interspersing of integers by reals
  • $(\forall x \in R) (\exists! n \in Z) n \leq x \lt n+1$
  • Integer part $n = \lfloor x \rfloor$
• (Excercise 5.4.8) LIM preserves order
  • Let $(a_n)_{n=0}^{\infty}$ be a Cauchy sequence of rationals; let $x$ be real
  • $(\forall n \in N) a_n \leq x \implies LIM_{n \rightarrow \infty}a_n \leq x$

Least upper bound

• (Definition 5.5.1) Upper bound
  • Let $E \subseteq R, M \in R$
  • $M$ is upper bound for $E \iff (\forall x \in E) x \leq M$
• (Definition 5.5.5) Least upper bound
  • Let $E \subseteq R, M \in R$
  • $M$ is least upper bound for $E$ iff:
    1. $M$ is upper bound for $E$
    2. $(\forall M’) [$ $M’$ is upperbound for $E \implies M’ \geq M]$
• (Proposition 5.5.8) Uniqueness of least upper bound
  • Let $E \subseteq R$, $E$ can have at most one least upper bound
• (Theorem 5.5.9) Existence of least upper bound
  • Let $E \subseteq R \land E \neq \emptyset$
  • $E$ has upper bound $\implies$ $E$ has exactly one least upper bound
• (Definition 5.5.10) Supremum
  • d

Test

Markdown rendering in Github page is buggy. It sometimes treat the underscore inside $ $ as italic and insert html tags that breaks later latex rendering.

$

x

$ $|x|$: | inside $ is treated as table delimiter

$$	x	$$
$$|x|$$: works

$(a_n)_{n=0}$ $(a_n)_{n=0}$ works

$(a_n){n=0}^\infty (a_n^{-1}){n=0}^\infty$

$(a_n)_{n=0}^\infty (a_n^{-1})_{n=0}^\infty$ doesn’t work. it matches up the _ as italic.

https://nschloe.github.io/2022/05/20/math-on-github.html https://stackoverflow.com/q/77375192/2797254

When $a \ne 0$, there are two solutions to $(ax^2 + bx + c = 0)$ and they are \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) \(R_{\mu \nu} - {1 \over 2}g_{\mu \nu}\,R + g_{\mu \nu} \Lambda = {8 \pi G \over c^4} T_{\mu \nu}\) $\frac1{x^{n}x^{m}} = \frac1{x^{n+m}} = x^{-n-m}$

The Cauchy-Schwarz Inequality \(\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)\)

inline $\left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)$

This sentence uses $ delimiters to show math inline: $\sqrt{3x-1}+(1+x)^2$

This site is open source. Improve this page.